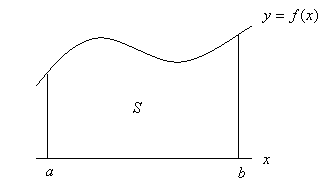
上のグラフにおいて、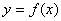
と
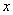軸に囲まれた区間[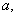
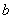]の面積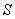
は、積分を用いて次のように計算することができることを数学IIで学習しました。
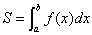
しかし、積分計算をコンピュータで行うのは難しいため、ここでは台形の面積による近似を利用して面積 を計算することを考えます。
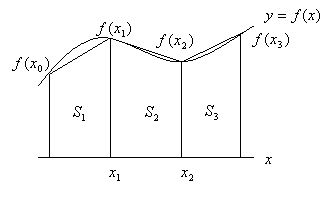
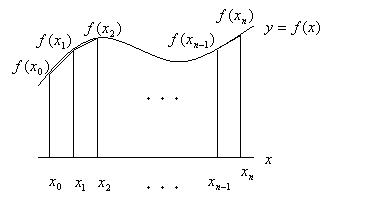
まず、上のグラフのように大ざっぱに3つの台形に分けてみました。そのため、次の関係が成り立ちます。
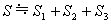―――(1)
これは、曲線と直線で囲まれた部分の面積のおおよその値（近似値）は台形の面積の和で表せることを意味しています。
そして、台形の面積は
(上底＋下底)×高さ÷2
と求められることから、台形の面積を計算することができます。
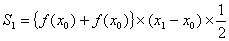―――(2)
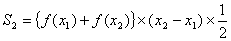―――(3)
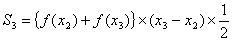―――(4)
ここで、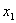
と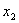
が等間隔にあり区間[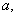 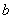]を3等分していると仮定するとその間隔
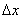は
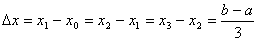
が成り立つので、式(1)〜(4)から
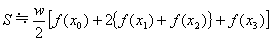
次に、台形で近似する際に生じる誤差について考えます。先ほどは簡単のため台形3つに分けて計算しましたが、このときに生じる誤差は左のグラフのようになります。青は面積が足りない部分で、赤は逆に面積を余分に求めてしまっている部分を表しています。
ここで、区間を8等分したグラフ（右）と比較してみます。すると、3等分したときと比べて誤差が減っています。つまり、区間を 等分したとき、 が大きいほど誤差の少ない正確な近似が行えることがわかります。
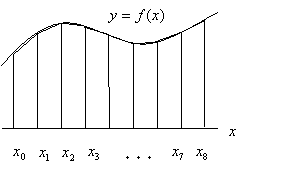
先ほどの3等分の例と同様に考えることで、区間を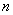
等分したときの面積を台形による近似計算で求める公式を導くことができます。
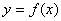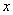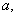
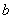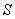と軸で囲まれた区間[ ]の面積は、区間を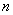等分して、その間隔を
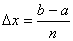等分とおくと
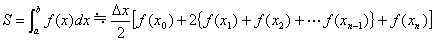
となります。
[例1]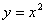 
と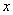軸で囲まれる区間[0, 1]の面積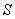を求める。
区間[0, 1]を10等分、すなわち、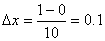
として近似計算します。
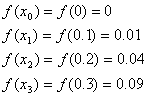
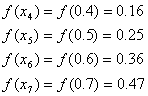
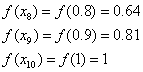
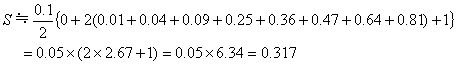
これは、積分で計算した値
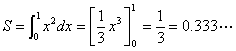
に近くなっていることが確認できます。
[例2]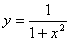 
と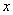軸で囲まれる区間[0, 1]の面積 を求める。
例1は人間が普通に計算した方が早く、台形公式のありがたみを感じることができなかったと思います。そこで、例2では数学IIまでの範囲では計算が不可能な積分を行います。これは、数学IIIを学習すれば計算できるようにはなりますが、それでも面倒で、大学生になって初めて簡単に計算ができる積分なので、台形公式を利用する価値は十分にあると言えるでしょう。
区間[0, 1]を10等分、すなわち、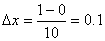として近似計算します。
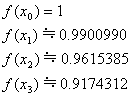
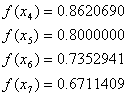
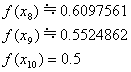
これは、積分で計算した値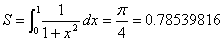
と非常に近い値となっています。
さて、台形公式の有用性は確認できましたが、人間が台形公式で計算をすると非常に面倒なのでプログラムを考えてコンピュータに計算させましょう。
[プログラム]
100 INPUT "n=";N
110 LET A=0
120 LET B=1
130 LET DX=(B-A)/N
140 LET S=0
150 FOR X=A TO B STEP DX
160 LET FX=1/(1+X^2)
170 IF X=A OR X=B THEN LET S=S+FX ELSE LET S=S+2*FX
180 NEXT X
190 S=S*DX/2
200 PRINT "S=";S
210 END
[実行結果]
n=10の場合
n=10 S= .78498149722679
n=100の場合
n=100 S= .785393996730785
n=1000の場合
n=1000 S= .78539812173074
[解説]
実行結果を見ると、nの値を増やすほど正しい値に計算結果が近づいていくことがわかります。
170行目のORは数学における「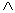
」（または）の働きをします。
なお、このプログラムでは しか計算できませんが、160行目を書き換えることによって別の関数を、110,120行目を書き換えることによって別の区間を計算することができます。